2023. 10. 10. 18:25ㆍRun/Computer Graphics

- 3D shape에는 Viewing, Lighting, Texture가 더해져야 한다.
- 이전까지 transformation(이동, 크기 변환, 회전 등)을 했다면, Viewing을 통해 카메라를 설정해보자.
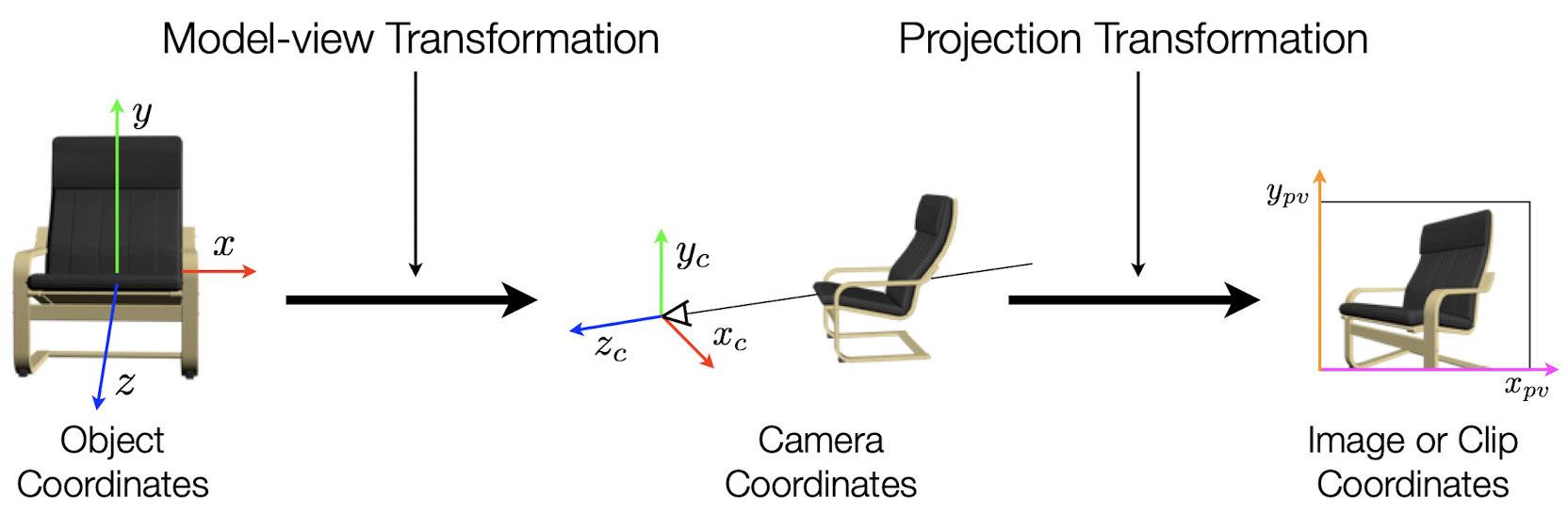
- Model-view Transformation은 Transformation 파트에서 진행한 부분이고, Viewing 파트에서는 Projection Transformation을 다룬다.
- Projection: Taking 3D information and collapsing it to 2D using an eye or camera.
Two Types of Projections
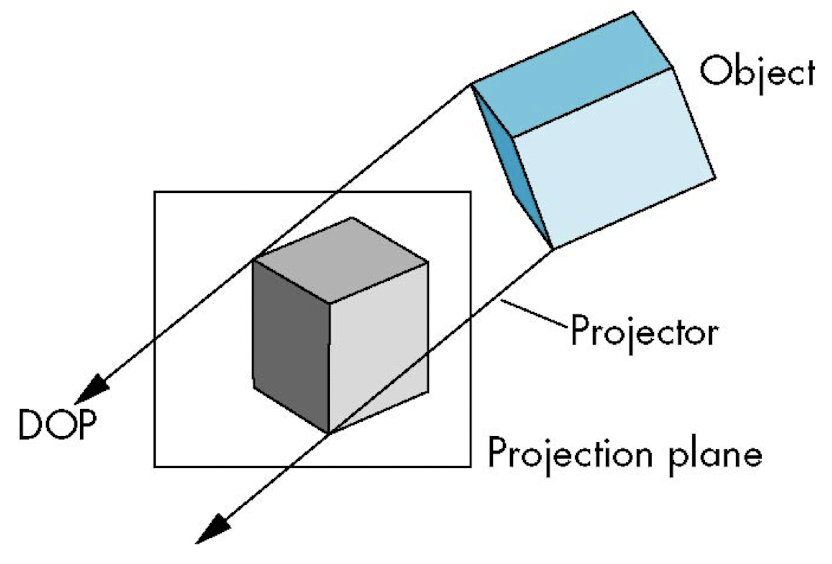
- 1) Parallel Projection: Projectors are parallel. The lines specify a direction of projection(DOP).
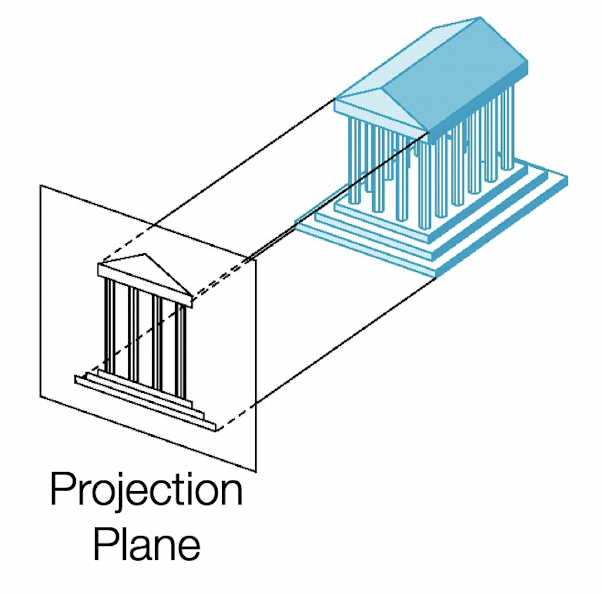
- 1-1) Parallel Orthographic Projection: Projections are each parallel to principal face of the object. Show more than 1 principal face of the object.
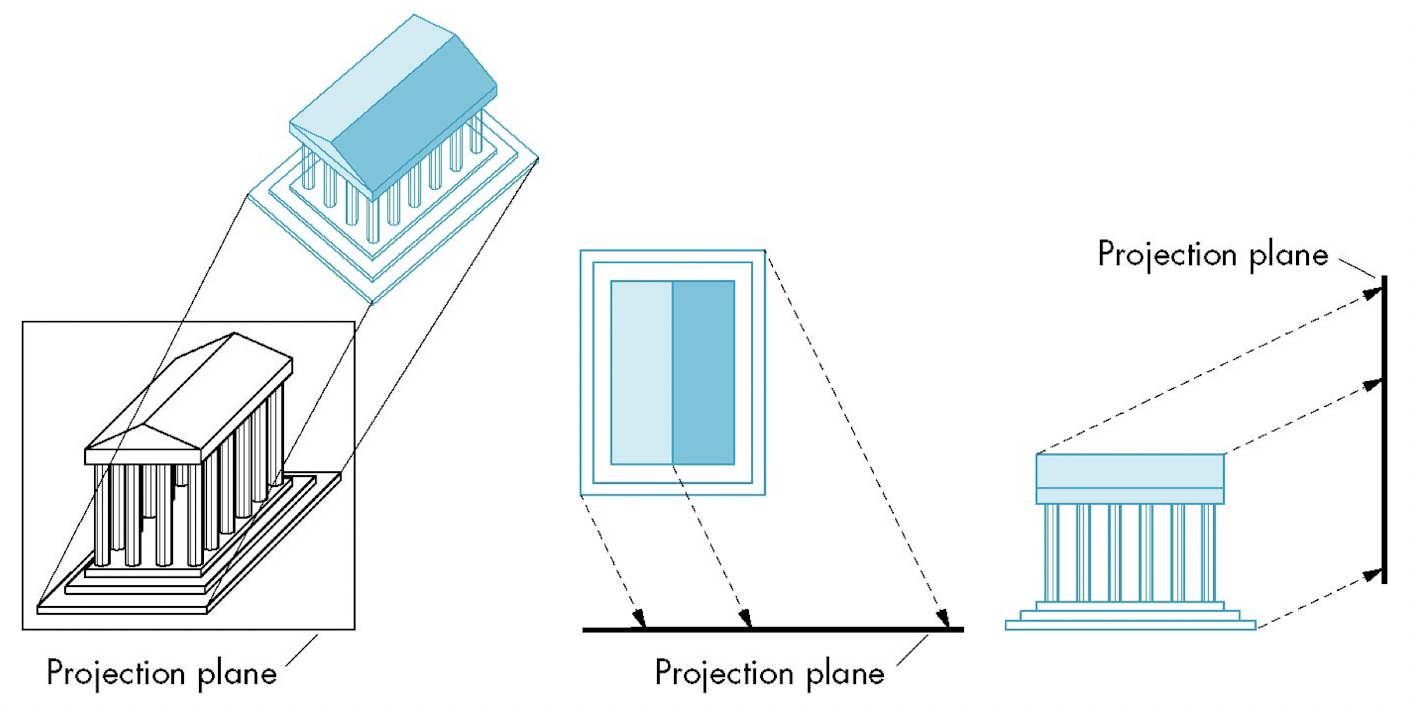
- 1-2) Parallel Oblique Projection: Projectors make a non right-angle with projection plane.
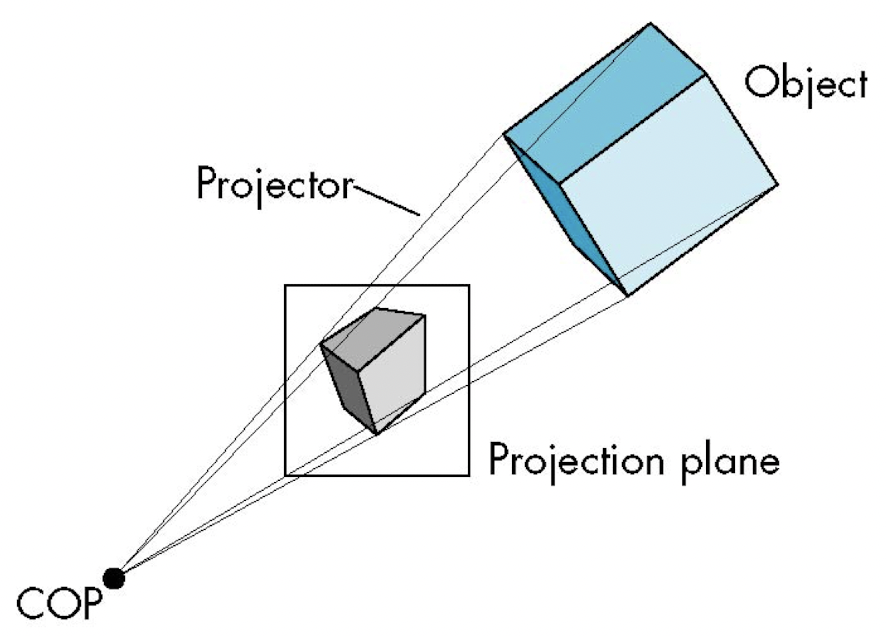
- 2) Perspective Projection: Projectors meet at a point called center of projection(COP).
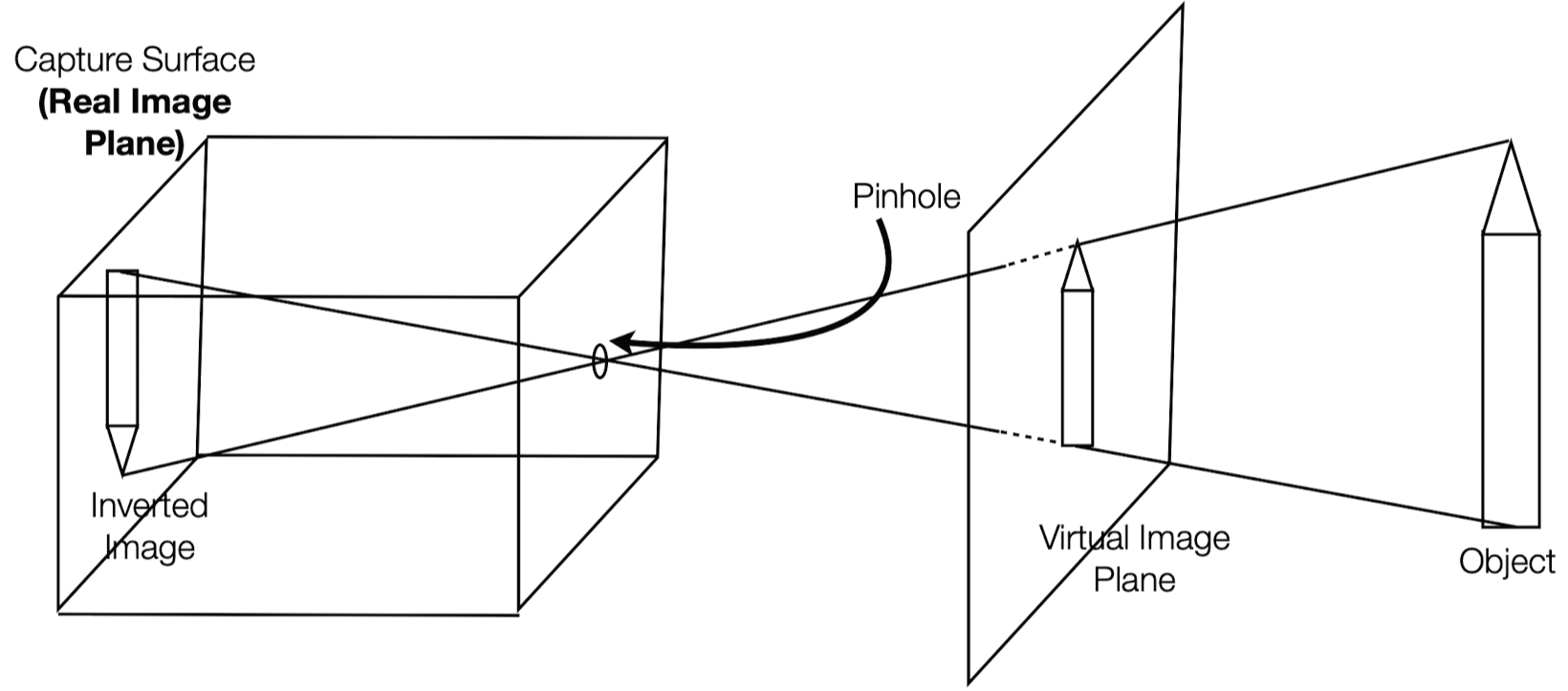
- 이미지가 Real Image Plane에 생성되지만, 뒤집혀 있다.
- Computer Graphics에서는 뒤집히지 않은 이미지를 보여주는 Virtual Image Plane을 사용한다.
- Virtual Image Plane에는 실제로 이미지가 생성되는 것은 아니다.
As the object moves away from the camera, its size on the projection plane:
- Parallel Projection: remains the same
- Perspective Projection: decreases
- Real cameras and eyes perform perspective projection.
Positioning the Camera
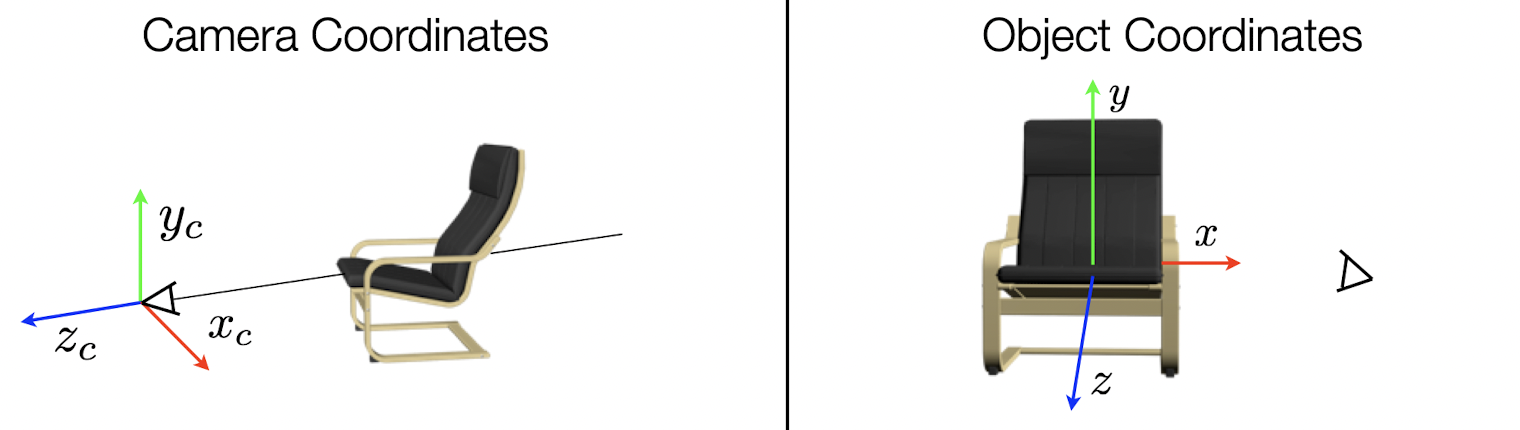
- Camera와 Object를 position하는 방법에는 2가지가 있다.
1. Camera Coordinates: keep the camera at the origin & move the object using model-view transformation.
2. Object Coordinates: keep the object at the origin & move the camera using inverse of the model-view transfomration.
- 두 방법 모두 동일한 이미지를 만들어 내고, WebGL에서는 Camera Coordinates 방식을 사용한다.
Camera: at the origin (0, 0, 0)
x-axis & y-axis of the camera: aligned with the image
z-axis of the camera: points out the image
- Model-view transformation을 정의하고, 카메라를 절대 움직이지 않는 방식으로 구현할 수도 있고,
- Look-at approach를 통해 camera를 위한 inverse model-view transformation을 정의하고, object를 위해 이를 model-view transformation으로 변환하는 방식으로 구현할 수도 있다.
Look-At Approach
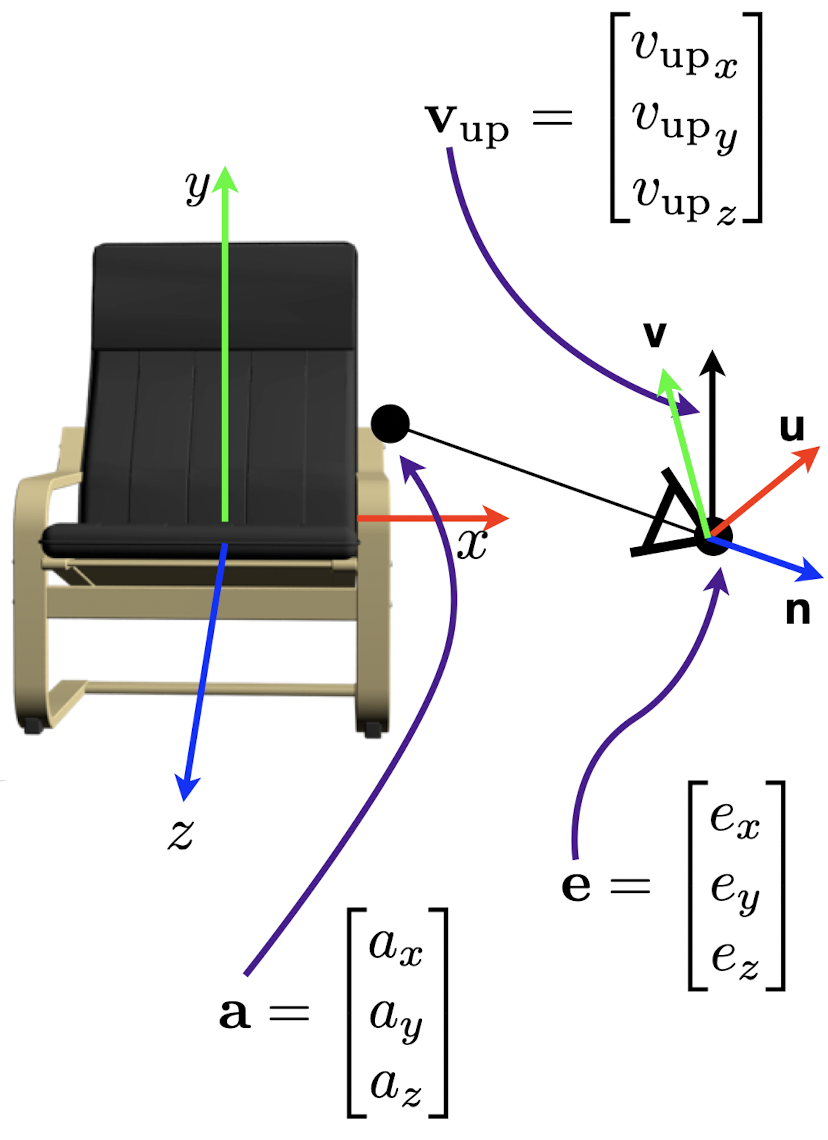
- Look-At Approach에서는 3가지 요소를 정의한다.
1. Eye (View Reference Point): e
2. Look At Point: a
3. Up Vector: vup
- 그 뒤, Object Coordinates를 계산한다.
1. View plane normal: n
2. View plane horizontal axis: u
3. View plane vertical axis: v
d = e - a, n = d / | d |
k = vup x n, u = k / | k |
l = n x u, v = l / | l |
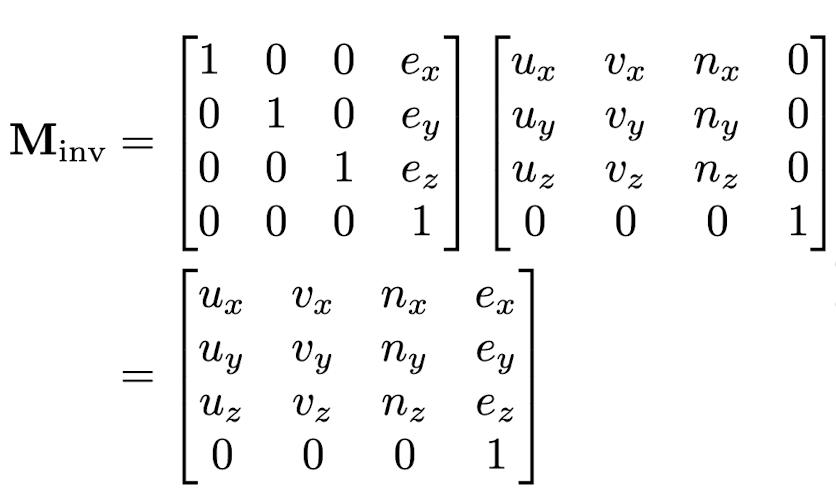

- 이렇게 정의한 것들을 inverse model-view transformation Minv를 설정하고 model-view transformation으로 변환하는 데 사용한다.
Projection Transformation
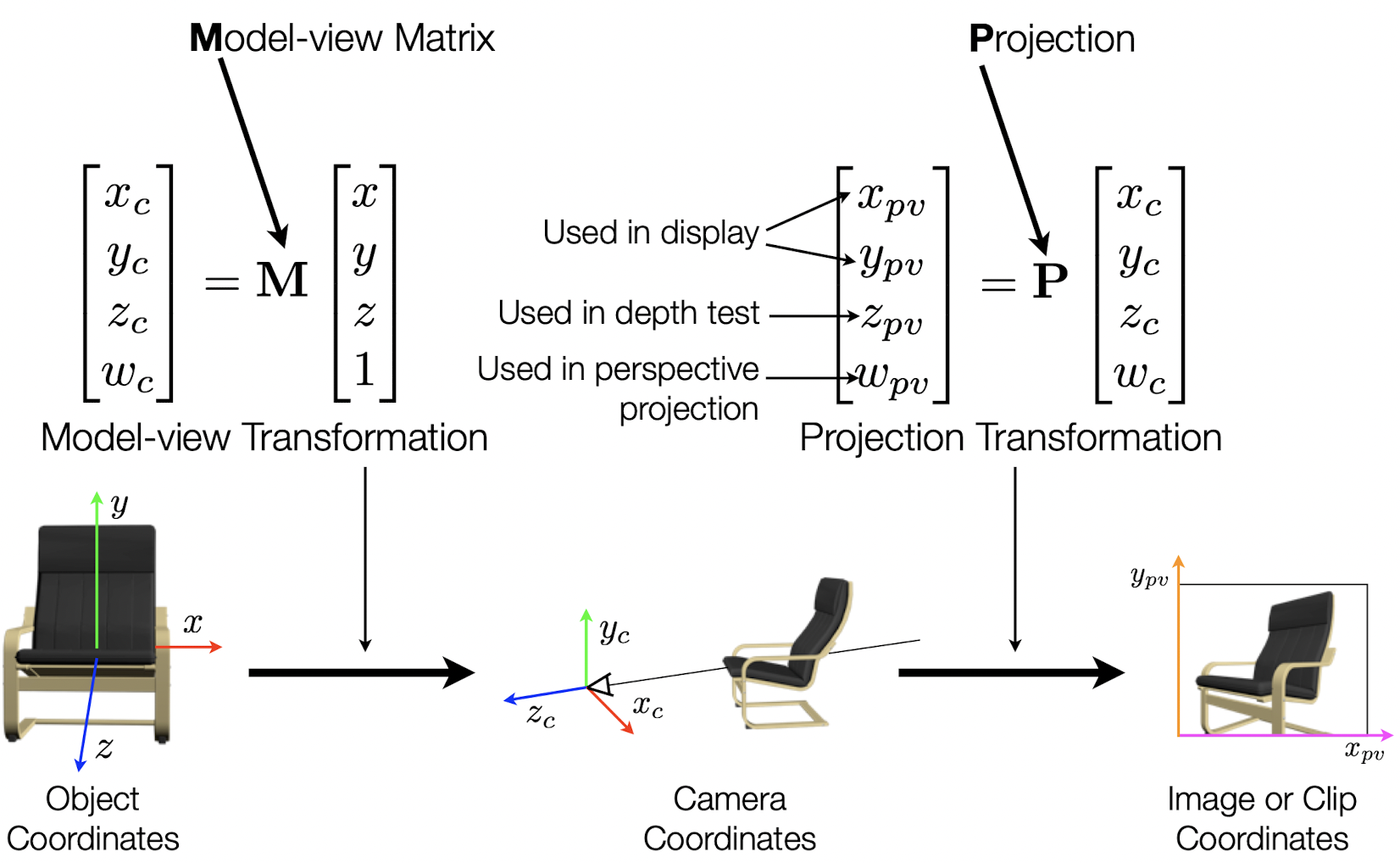
1. Parallel Orthographic Projections
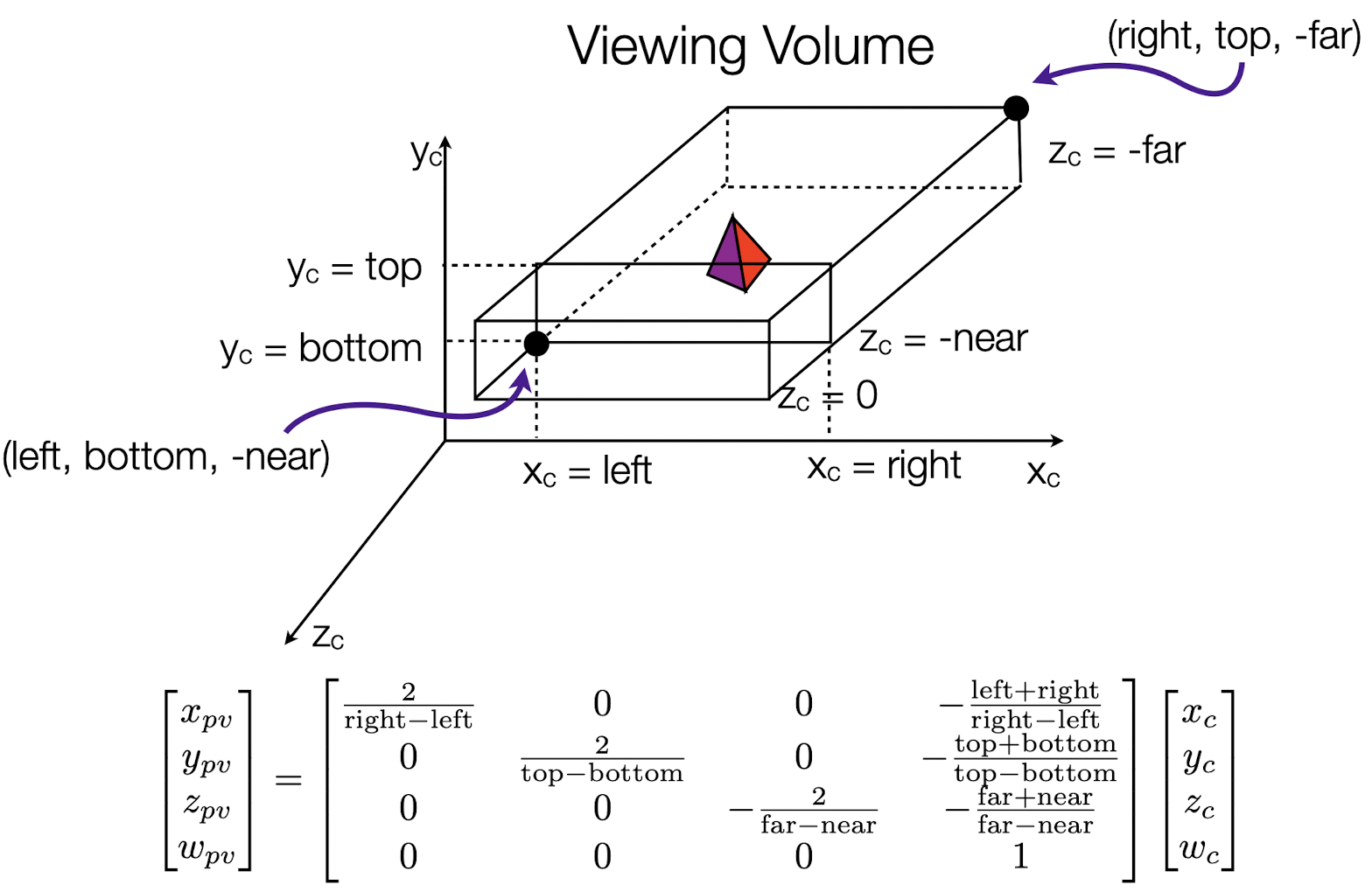
- Left plane, right plane, top plane, bottom plane, near plane, far plane을 정의한다.
- xpv, ypv, zpv의 범위는 -1 ~ 1 이어야 한다. 도형의 모든 부분이 WebGL viewport에서 보여야 하기 때문이다. (Normalizing transformation)
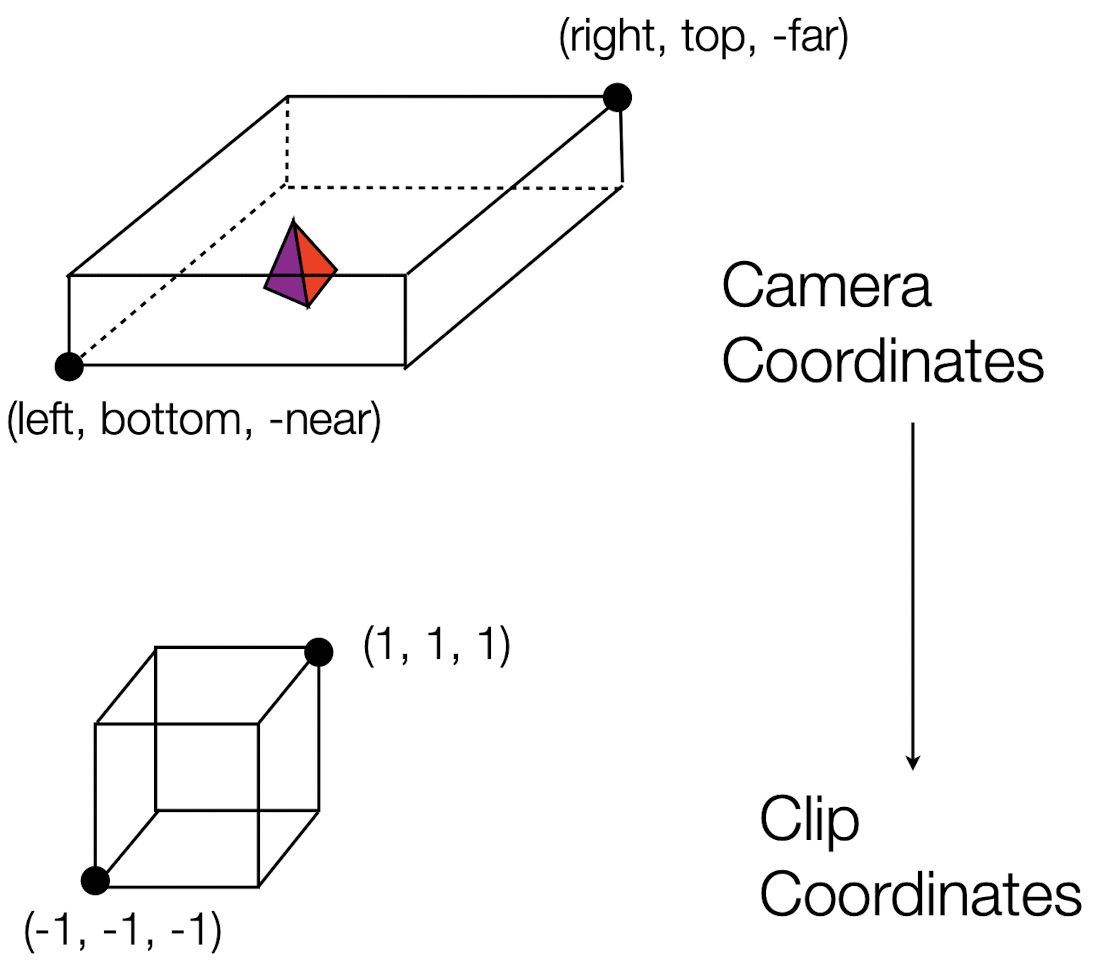
- left: +ve or -ve
- right: +ve or -ve
- top: +ve or -ve
- bottom: +ve or -ve
- near: +ve
- far: +ve
- Camera Coordinates (Right-handed coordinate system) → Clip Coordinates (Left-handed coordinate system)
- z coordinate = 렌더링된 pixel들을 정렬하는 데 사용 (depth)
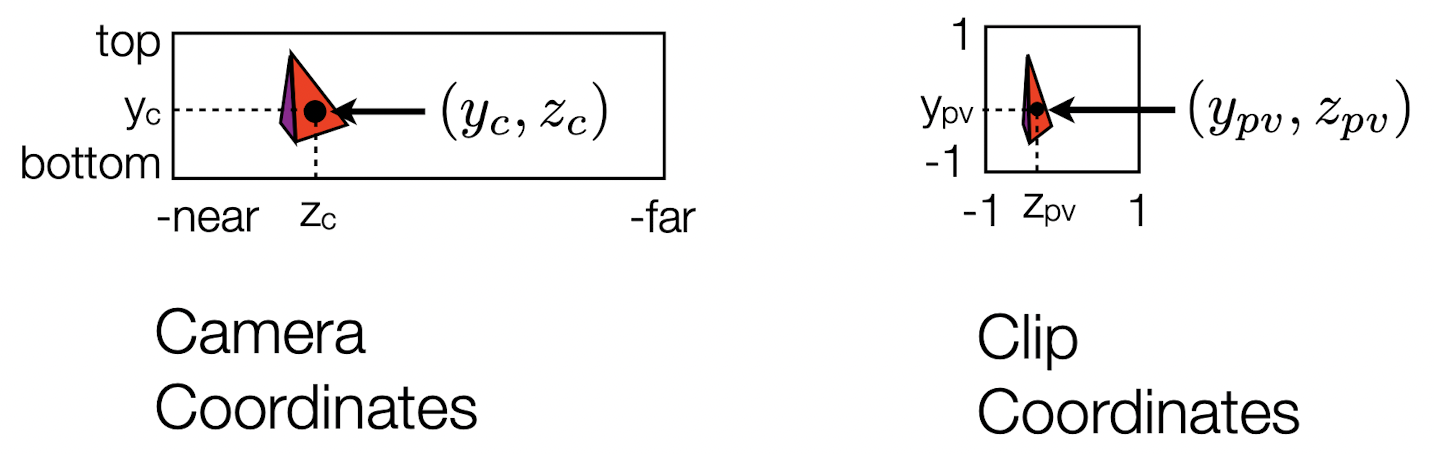
- 측면에서 본 Parallel Projection
2. Perspective Projections
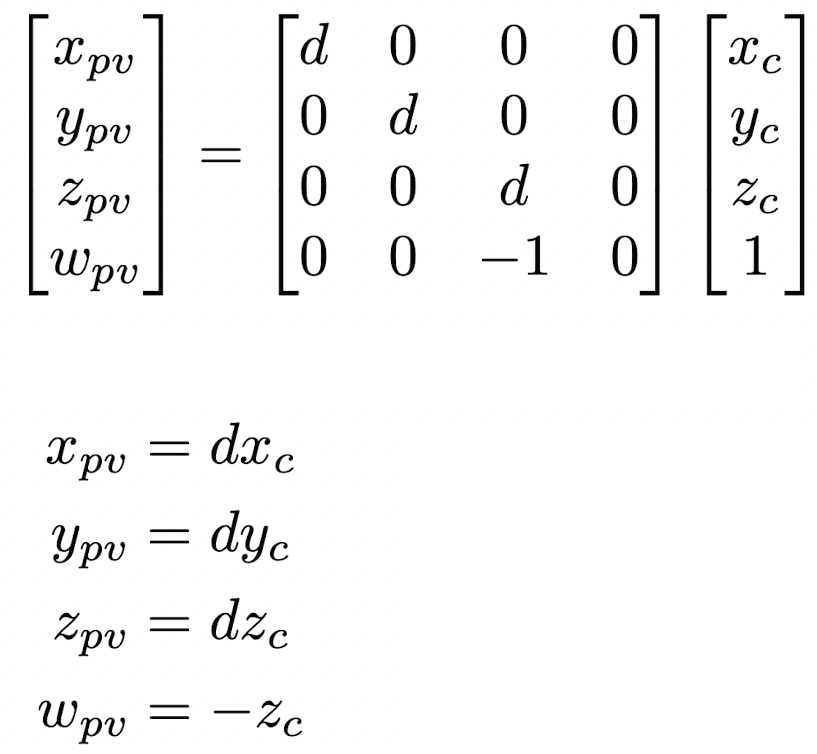
- 왼쪽은 Projection Equation이다.
- 오른쪽의 Matrix-vector multiplication을 통해 individual equations을 구할 수 있다.
- wpv 값이 1이 아니기 때문에 모든 값을 wpv(-zc)로 나눠준다.
(→ represents shrinking of an object as it moves away from a camera)
- 이는 WebGL에서 알아서 해주기 때문에 따로 w를 나눌 필요는 없다.

- 그럼 이와 같은 값을 얻을 수 있다.
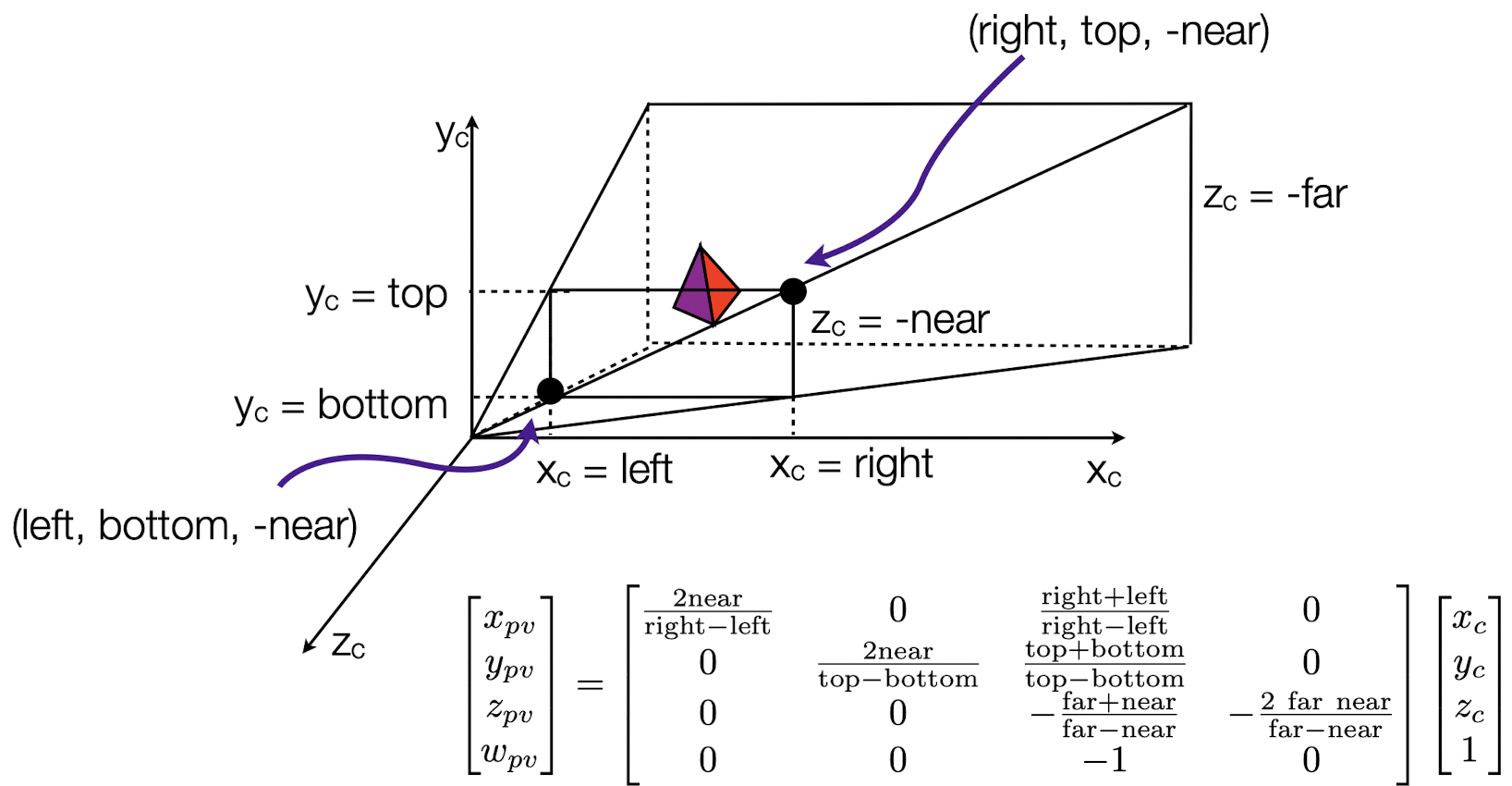
- left: +ve or -ve
- right: +ve or -ve
- top: +ve or -ve
- bottom: +ve or -ve
- near: +ve
- far: +ve
- Projection의 중심이 (-near) 앞에 있고 도형 전체의 모습을 나타내려면 near과 far이 무조건 양수여야 한다.
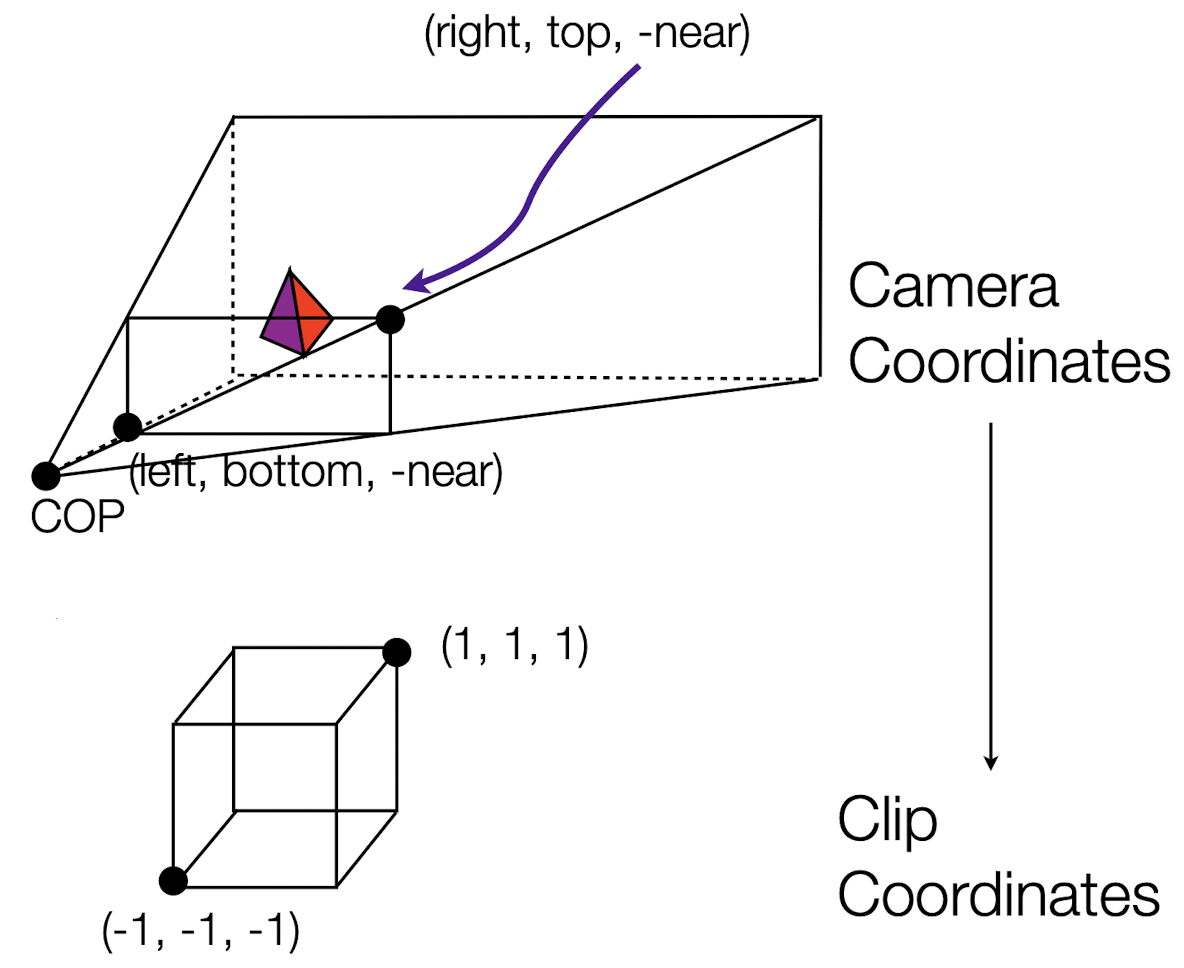
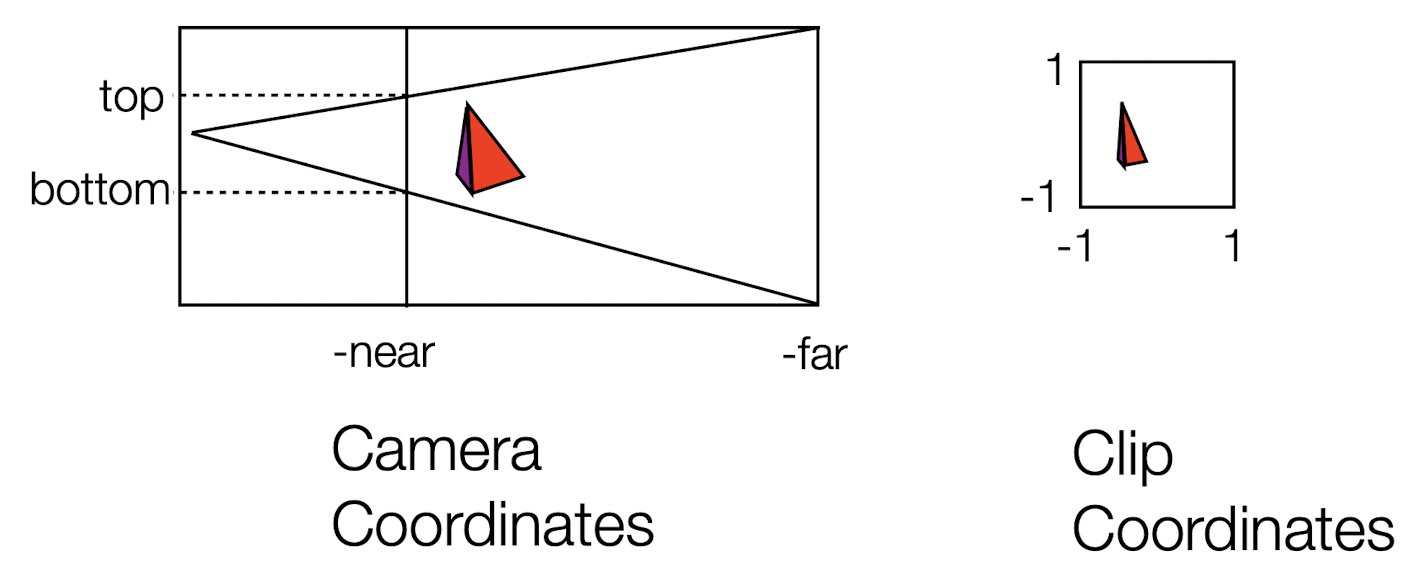
- 측면에서 본 Perspective Projection
What to do in WebGL?
- set up projection matrix P for projection (parallel or perspective)
- multiply projection matrix P to left of model-view matrix M
- vf = P * M * vi;
'Run > Computer Graphics' 카테고리의 다른 글
| [Computer Graphics] Texture Mapping (0) | 2023.10.10 |
|---|---|
| [Computer Graphics] Lighting (1) | 2023.10.10 |
| [Computer Grpahics] WebGL Variables (0) | 2023.10.10 |
| [Computer Graphics] WebGL 다각형 그리기 (0) | 2023.10.10 |
| [Computer Graphics] WebGL 삼각형 그리기 (1) | 2023.10.10 |