2023. 10. 11. 00:03ㆍRun/Algorithm
✔️ Searching Algorithm
1) 자료 탐색?
- 수많은 자료 중 원하는 자료 찾는 작업
- 컴퓨터에서 처리되는 핵심 알고리즘 중 하나
- Search Key (탐색 키): 탐색할 때 기준이 되는 값 (항목과 항목을 구별하는 값)
- 사용되는 자료구조: 배열, 연결 리스트, 트리, 그래프 등
- ex) 컴퓨터에서 저장된 파일 찾기: 파일 탐색기, 위치 모르면 완전 탐색 (exhaustive search)
2) 자료 탐색 과정
1) 탐색 기준 정하기: 탐색 키 선정
2) 자료 비교하기: 탐색 키와 자료 리스트에 포함된 자료들의 비교 ⭐️
3) 자료 찾기: 탐색의 성공, 실패에 대한 판가름
3) 자료 탐색 결과
- 존재하는 경우: 탐색 키에 해당하는 인덱스 번호 반환
- 존재하지 않는 경우: 일반적으로 -1 반환, Python은 오류 처리
4) 정렬과 탐색의 관계
- 정렬된 상태에서의 탐색 작업: ex) [-7, -4, 1, 5, 9]
- 정렬되지 않은 상태에서의 탐색 작업: ex) [5, -7, 9, 1, -4]
✔️ 선형 자료 탐색
1) 이진 탐색 (Binary Search)
- 정렬된 상태인 경우 사용
1) 중간 값과 비교하여 작으면 중간 값 앞부분을, 크면 뒷부분을 비교
2) 다시 중간 값을 찾아 비교
3) 반복
2) 순차 탐색 (Sequential Search)
- 정렬되지 않은 상태인 경우 사용
- 순서대로 앞에서부터 하나씩 비교
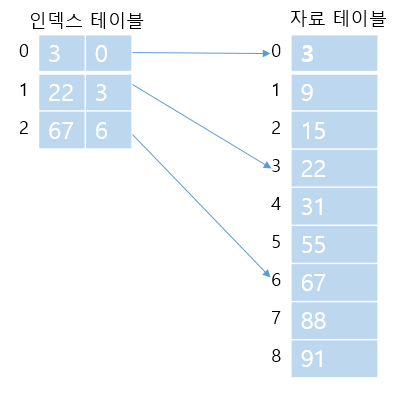
3) 색인 순차 탐색 (Indexed Sequential Search)
- 인덱스를 사용하는 정렬된 상태의 경우
- 인덱스 테이블을 추가로 사용하여 탐색 효율 증대
- 주 자료 리스트, 인덱스 테이블은 모두 정렬되어 있어야 함
1) 기준 값을 인덱스 테이블의 자료 값에서 검색
2) indexTable[i] <= key < indexTable[i + 1]
3) i를 찾아서 i ~ i+1까지 주 자료 테이블에서 비교
✔️ 비선형 자료 탐색
1) Binary Search Tree
1) BST 조건에 따라 검색
- 왼쪽 subtree는 root보다 작은 값
- 오른쪽 subtree는 root보다 크거나 같은 값
2) 반복하여 해당 subtree에서 탐색
2) 배열 → 이진 탐색 트리

3) 배열 vs 이진 탐색 트리

4) 깊이 우선 탐색 (Depth First Search)
- 시작 node에서 연결된 edge가 존재하는 경우 계속하여 깊게 들어가며 탐색하는 알고리즘
- 깊게 들어가다가 최하위 레벨에 해당하는 node(= leaf)에 도달하면 backtracking을 적용하여, 다른 연결된 가장 가까운 node로 이동
- Stack 사용
5) 너비 우선 탐색 (Bredath First Search)
- Root부터 시작하여 깊이가 1인 모든 node를 우선 비교 탐색 (그 다음 깊이 2, 깊이 3, ...)
- Queue 사용

✔️ Sorting Algoirhtm
1) Sorting Algorithm
- 자료를 원하는 기준에 맞게 순서를 재배치
- 자료 처리의 효율성을 향상시키기 위한 작업
- 다양한 정렬 방법 중 상황에 맞는 알고리즘 선택하여 적용
2) Sorting 과정 비교

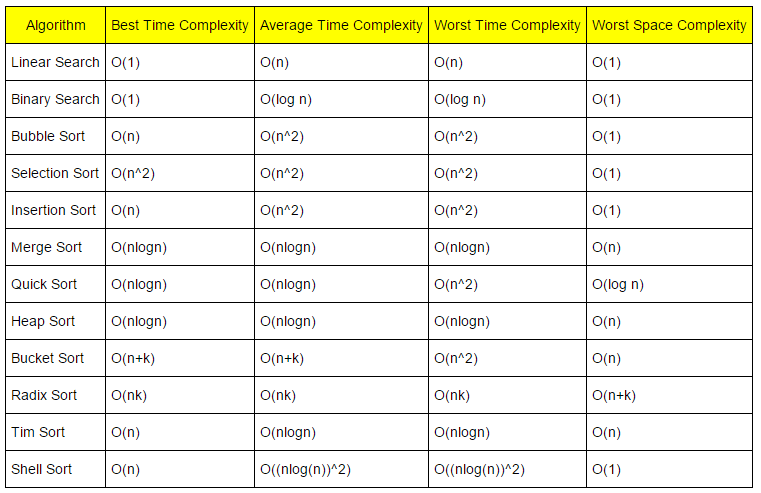
✔️ 다양한 정렬 알고리즘
1) 선택 정렬 방식 (Selection Sort)
- 앞에서부터 차례대로 정렬하는 방식
- 주어진 배열에서 최솟값을 찾고, 그 값을 맨 앞에 위치한 값과 교체

2) 버블 정렬 방식 (Bubble Sort)
- 첫 번째 원소부터 인접한 원소끼리 계속 자리를 교환하며 정렬하는 방식

3) 삽입 정렬 방식 (Insertion Sort)
- 주어진 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 부분과 비교하여 자신의 위치를 찾아 삽입하는 방식

4) Heap 정렬 방식 (Heap Sort)
- 완전 이진 트리: 최대 2개의 자식 노드를 갖는 이진 트리 중 노드가 왼쪽부터 차례대로 채워져 있는 트리
- 최대 힙 (max heap): 부모 노드 키 값 ≥ 자식 노드 키 값. 루트 노드 키 값 가장 큼
- 최소 힙 (mean heap): 부모 노드 키 값 ≤ 자식 노드 키 값. 루트 노드 키 값 가장 작음

- 완전 이진 트리 형태 생성 → 최대 힙(내림차순 정렬) or 최소 힙(오름차순 정렬)으로 reconstruct

5) 빠른 정렬 방식 (Quick Sort)
- (Pivot보다 작은 숫자들) (Pivot) (Pivot보다 큰 숫자들)
- 분할된 부분 문제들에 대해 동일 과정을 재귀적으로 수행하여 정렬

6) 합병 정렬 방식 (Merge Sort)
- 작은 단위로 쪼개 작은 단위부터 정렬해서 정렬된 단위들을 계속 병합해가는 방식
1) 분할(divide): 문제를 최소 단위로 분할
2) 정복(conquer): 작은 단위의 문제 해결
3) 통합(combine): 통합하여 원래 문제의 답 찾기

'Run > Algorithm' 카테고리의 다른 글
| [Algorithm] 4. Divide and Conquer (1) | 2023.10.11 |
|---|---|
| [Algorithm] 3. Brute Force Algorithm (0) | 2023.10.11 |
| [Algorithm] 1. Data Structure 복습 (0) | 2023.10.11 |
| [Algorithm] 0. Introduction (0) | 2023.10.11 |
| [Algorithm] 빅오(Big-O) 표기법 (0) | 2023.10.11 |