2023. 10. 10. 18:19ㆍRun/Etc

Extended Euclidean Algorithm, Chinese Remainder Theorem, Fermat's Little Theorem 을 이용하여 RSA decryption 을 진행해보자.

| 주어진 조건 - n = 2491 - C = 1644 (mod 2491) - e는 최대한 작은 홀수 - p < q |
풀이 과정 1) p, q 계산 2) φ 계산 3) e, d 계산 - Extended Euclidean Algorithm (Pulverizer of Aryabhata) 4) M (mod p), M (mod q) 계산 - Fermat's Little Theorem 5) M (mod n) 계산 - Chinese Remainder Theorem, Extended Euclidean Algorithm |
1) p, q 계산
n = p * q 이다. 주어진 n의 값이 그렇게 크지 않아서 p와 q를 쉽게 구할 수 있다.
p * q = 2491, p < q 이므로 p = 47, q = 53 이다.
2) φ 계산
φ = (p - 1) * (q - 1) 이다. 따라서 φ = 2392 이다.
3) e, d 계산
RSA에서 gcd(φ, e) = 1, 즉 e와 φ의 최대공약수는 1이며 (혹은 e와 φ는 서로소이며)
ed ≡ 1 (mod φ), 즉 e와 d를 곱한 수는 φ로 나눠 떨어지지 않는다.
Extended Euclidean Algorithm (확장된 유클리드 알고리즘, XGCD)을 사용하면 e, d를 더 쉽게 구할 수 있다.
gcd(φ, e) = 1 = Xφ + Ye 를 만족하는 X, Y는 항상 존재한다. 이때 Y는 d이며, X, Y 값은 Extended Euclidean Algorithm으로 구한다.
우선 e는 최대한 작은 홀수여야 하고, φ와 서로소 관계에 있어야 한다. 따라서 e = 3 이다.
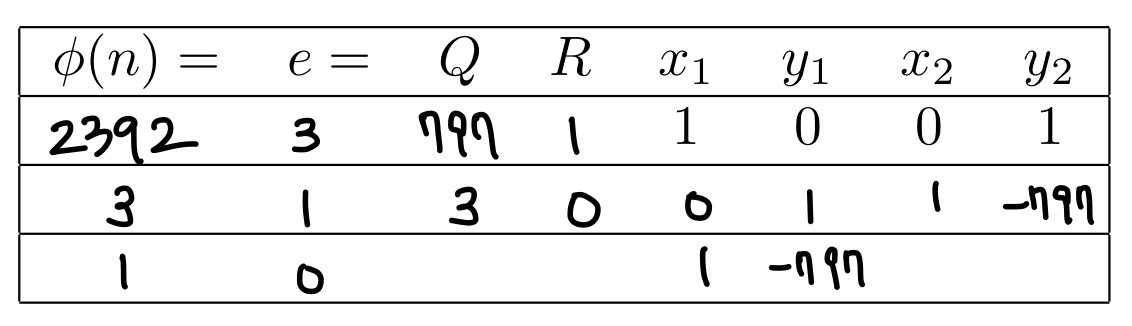
Q는 몫, R은 나머지이다. x1, y1, x2, y2는 맨 첫 줄에서 1, 0, 0, 1로 적고 계산을 시작한다.

이전 줄의 x2, y2 값은 다음 줄의 x1, y1 값으로 설정된다.
x2 값은 이전 줄의 x1, Q, x2 값을 이용해 구한다. (x1 - Q * x2)
y2 값은 이전 줄의 y1, Q, y2 값을 이용해 구한다. (y1 - Q * y2)
gcd 계산을 진행할 수 없을 때까지 계산을 반복한다.
최종적으로, gcd(φ, e) = 1 = Xφ + Ye,
gcd(2392, 3) = 1 = 1 * 2392 + (-797) * 3 이 성립하는 걸 확인할 수 있다.
따라서 d = -797 ≡ 1595 (mod 2392) 이다.
4) M (mod p), M (mod q) 계산
C = 1644, d = 1595 이다. 따라서, M = 1644^1595 (mod 2491) 이다.
M mod 47, M mod 53은 Fermat's Little Theorem을 이용하여 구할 수 있다.
1644와 지수 1595를 p, p-1, q, q-1로 나눈 나머지 값을 이용하면 된다.
1644 mod 47 = 46
1595 mod 46 = 31
1644 mod 53 = 1
1595 mod 52 = 35
위 계산에 의해
M ≡ 46^31 (mod 47)
M ≡ 1^35 (mod 53)
이 성립된다.
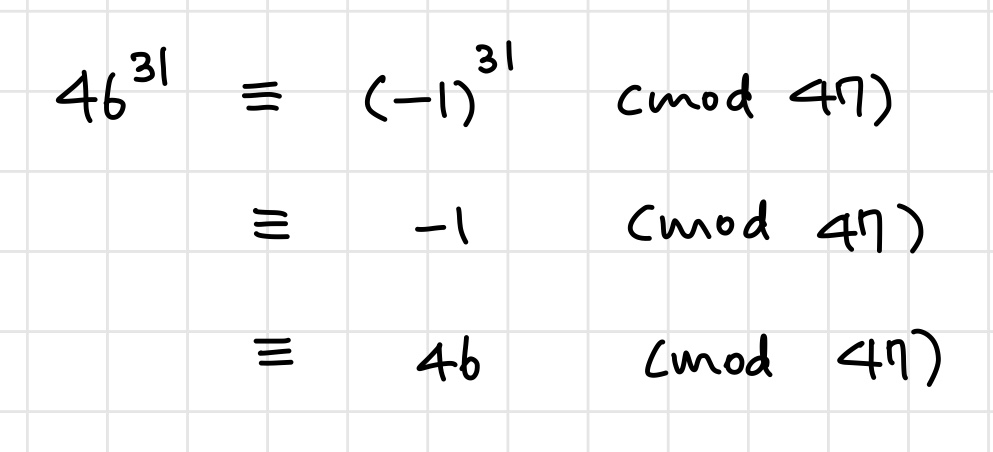
위 계산에 의해 M (mod p) = 46 이다. 1의 35승은 1이므로 M (mod q) = 1 이다.
5) M (mod n) 계산

ap, aq를 구하기 위해 Extended Euclidean Theorem을 다시 한 번 사용했다.
Chinese Remainder Theorem에 의해, M ≡ M (mod p) * ap + M (mod q) * aq 이 성립한다.
따라서, M ≡ 46 * 424 + 1 * 2068 ≡ 21572 ≡ 1644 (mod 2491) 이다.
따라서, 구하고자 하는 M의 값은 1644 이다.
C 값과 M 값이 같은 게 이상해서 교수님께 질문드렸더니, M을 정확하게 구했는지 확인하고 싶으면
다시 encryption C = M^e (mod n) 을 진행해보라고 하셨다.
다시 역으로 계산해보니 C 값이 1644로 나왔다. 정확히 구한 게 맞다.
풀이에만 집중하다보니 이론 증명 과정은 전부 생략했는데 나중에 시간 나면 추가해야겠다.
[ 요약 ]

'Run > Etc' 카테고리의 다른 글
| [Etc] Render Pipeline Converter 없음 (0) | 2023.10.11 |
|---|---|
| [Etc] Mitsuba Renderer 설치 (0) | 2023.10.11 |
| [Etc] NeRF-pytorch 코드 실행하기 (1) | 2023.10.10 |
| [Etc] LaTeX/Overleaf 사용팁 (0) | 2023.10.10 |
| [Etc] One-time Pad (0) | 2023.10.10 |