[Algorithm] 빅오(Big-O) 표기법
2023. 10. 11. 00:03ㆍRun/Algorithm
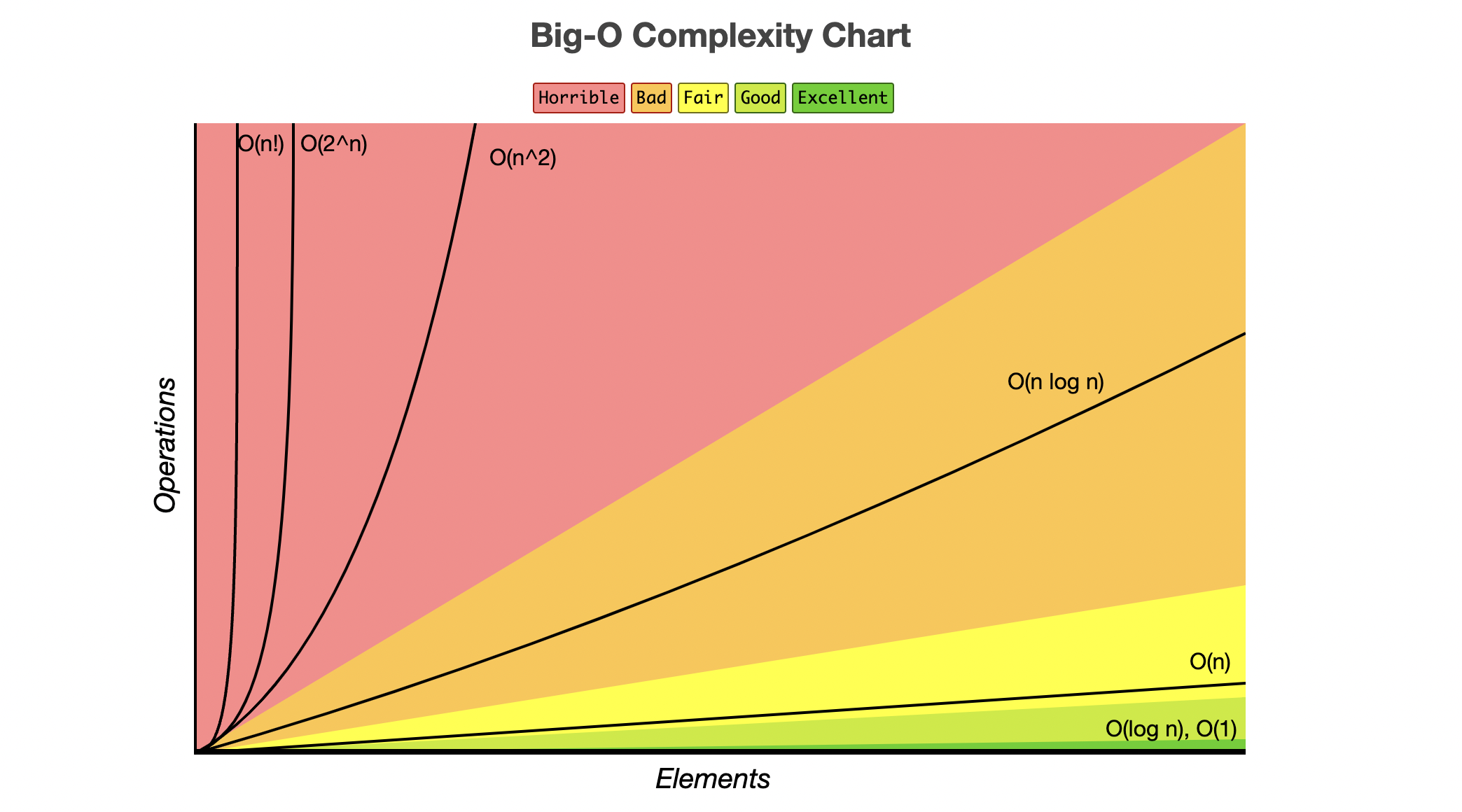
What is Big-O?
- Mathematical notation that describes algorithm efficiency
- Time & Space complexity
- Describes the growth rate of algorithms
- Big-O에서 상수는 버림 (ex. O(2n) → O(n), O(n^2 + n^2) → O(n^2))
∵ 알고리즘의 running time을 재기 위함이 아니라 데이터의 증가에 따른 처리시간 증가율을 예측하기 위함
O(1) : constant time
- 입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘
// 배열의 길이와 관계없이 언제나 일정한 속도로 결과 반환
F(int[] n) {
return (n[0] == 0) ? true:false;
}
O(n) : linear time
- 입력 데이터의 크기에 비례해서 처리 시간이 걸리는 알고리즘
F(int[] n) {
for i = 0 to n.length
print i
}
O(n^2) : quadratic time
F(int[] n) {
for i = 0 to n.length
for j = 0 to n.length
print i + j;
}
O(nm) : quadratic time
F(int[] n, int[] m) {
for i = 0 to n.length
for j = 0 to m.length
print i + j;
}
O(n^3) : polynomial / cubic time
F(int[] n) {
for i = 0 to n.length
for j = 0 to n.length
for k = 0 to n.length
print i + j + k;
}
O(2^n) : exponential time
- 대표 예: finbonacci sequence
// 피보나치 수열
// 함수 호출 시 바로 전 숫자, 전전 숫자를 알아야 하므로 매번 2번씩 더 호출됨
F(n, r) {
if (n <= 0) return 0;
else if (n == 1) return r[n] = 1;
return r[n] = F(n - 1, r) + F(n - 2, r);
}
O(log n)
- 대표적인 예: binary search
- 한 번 처리가 진행될 때마다 검색해야 하는 데이터의 양이 절반씩 떨어지는 알고리즘
// binary search
F(k, arr, s, e) {
if (s > e) return -1;
m = (s + e) / 2; // 배열의 중간값 찾기
if (arr[m] == k) return m;
else if (arr[m] > k) return F(k, arr, s, m - 1;
else return F(k, arr, m + 1, e);
}
O(sqrt(n))
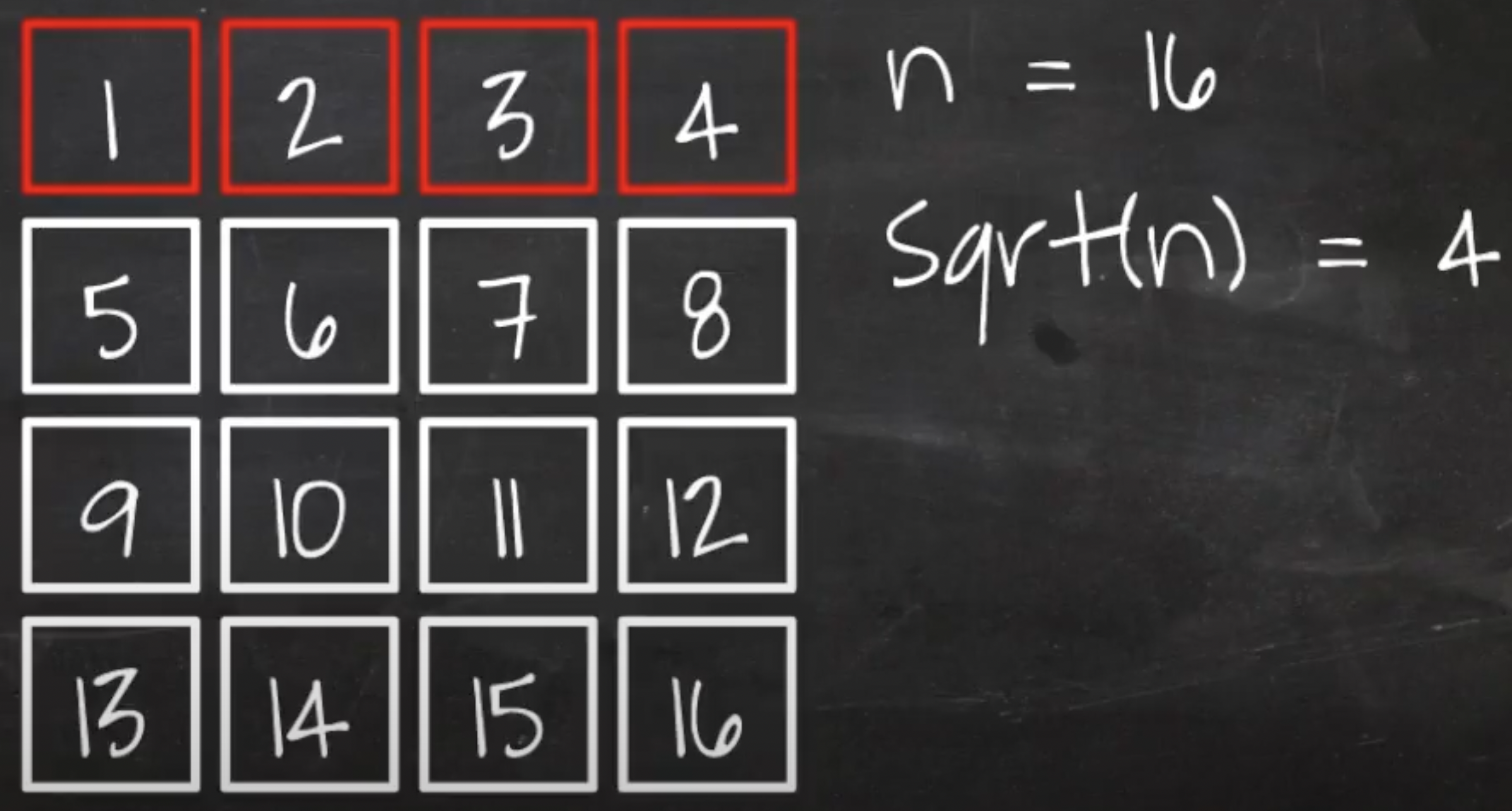
- 맨위 한 줄이 제곱근임 → 맨위 한 줄만 돌리는 알고리즘
참고자료
'Run > Algorithm' 카테고리의 다른 글
| [Algorithm] 4. Divide and Conquer (1) | 2023.10.11 |
|---|---|
| [Algorithm] 3. Brute Force Algorithm (0) | 2023.10.11 |
| [Algorithm] 2. 탐색과 정렬 알고리즘 (0) | 2023.10.11 |
| [Algorithm] 1. Data Structure 복습 (0) | 2023.10.11 |
| [Algorithm] 0. Introduction (0) | 2023.10.11 |