2023. 10. 14. 00:57ㆍRun/Machine Learning
Stanford University CS231n, Spring 2017
CS231n: Convolutional Neural Networks for Visual Recognition Spring 2017 http://cs231n.stanford.edu/
www.youtube.com

위 classifier는 첫 번째 이미지를 dog로, 두 번째 이미지를 automobile로, 세 번째 이미지를 truck으로 추측하고 있음
따라서 좋은 classifier가 아님, 우리가 원하는 것은 실제 정답인 class에 대해 가장 높은 score을 띄도록 하는 것
Weight를 사용하여 score을 구하고, 이를 바탕으로 weight가 얼마나 안 좋은지 측정하는 것이 loss function임
가능한 weight들 중 가장 적절한 weight를 구하는 과정이 optimization임

Score을 구하는 방법 $f(x, W) = Wx$

데이터셋의 구성
$x$는 이미지, $y$는 해당 이미지의 라벨 (정수값으로 매겨짐)

Loss function
모든 데이터셋에 대해 loss 값을 구한 뒤 평균을 냄
이 loss function은 가장 기본적인 형태이고, 이외에 여러 loss function이 있음 (ex. SVM loss)
Multiclass SVM Loss

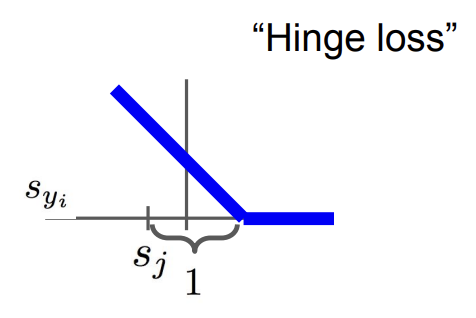
데이터셋 $(x_i, y_i)$
Scores vector: $s = f(x_i, W)$
정답 카테고리($y_i$)를 제외한 나머지 카테고리 $y$의 합을 구하고,
정답 카테고리의 score($s_{y_i}$)과 틀린 카테고리의 score($s_j$)을 비교함
만약 $s_{y_i}$가 $s_j$보다 특정 값 (safety margin, 위 예시에서는 1) 이상 크면, loss 값은 0이 되고
만약 특정 값 이상 크지 않으면, $(s_{y_i} - s_j +$ 특정 값$)$이 전체 loss에 더해지게 됨
Loss function을 보면 정답 카테고리의 score이 높을수록 loss가 선형적으로 줄어드는 것을 볼 수 있음


이를 모든 데이터셋에 대해 계산하고 평균을 구하면 최종 loss 값이 됨
모든 score이 0이라고 하면 loss 값은 'class 수 - 1'이 되는데, 이 특성은 디버깅할 때 유용함
Loss 값이 0이라고 해서 해당 weight가 유일한 것이 아님 (ex. 2*weight로 계산해도 loss 값 0임)
Regularization
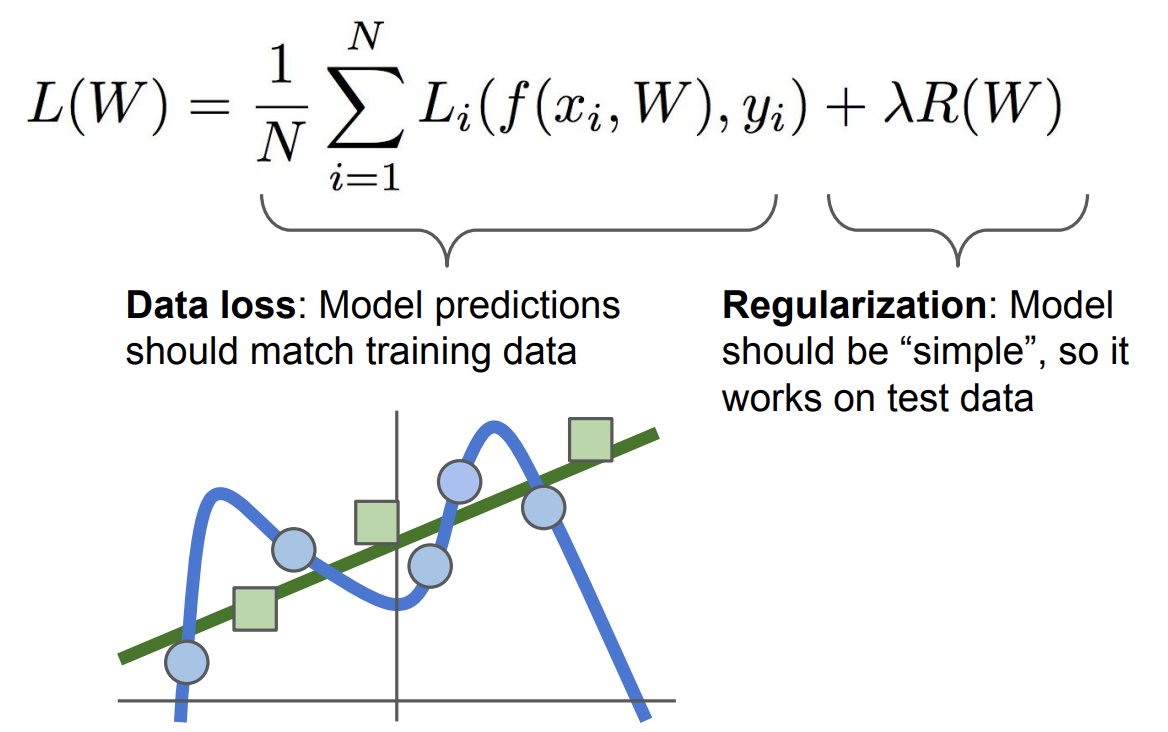
우리는 classifier가 test data에 대해 잘 작동하기를 원함
즉, 파란색 데이터에 맞춰 구불구불한 classifier가 되기 보다는, 초록색 데이터에 맞춘 classifier가 되기를 원함
이에 regularization 항을 추가해 classifier가 좀 더 단순한 weight를 찾을 수 있도록 함 ($\lambda$는 hyperparameter)


Regularization 종류는 여러 가지가 있음 (2017년 자료라 더 최신 방식이 있을 수도?)
L1 regularization은 weight에 0이 아닌 요소가 많은 복잡하고, 0이 많으면 덜 복잡함
L2 regularization은 weight가 어느 쪽에 치중되어 있으면 복잡하고, 전체적으로 퍼져있으면 덜 복잡함
Softmax Classifier (Multinomial Logistic Regression)

SVM loss에서는 score에 대해 분석을 하지 않았음
Multinomial logistic regression의 cost function은 score 자체에 의미를 부여함
Softmax 함수를 사용하여 score을 가지고 class 별 확률 분포를 계산함

각 score에 대해, exp를 취해 양수로 만들고 이를 normalize 함
이를 통해 확률 분포를 얻을 수 있고, 이는 input 이미지가 해당 class일 확률이 됨
확률이므로 값은 0~1 사이이고 모든 확률의 합은 1임
우리가 원하는 것은 정답 class의 확률이 최대한 1과 가까운 것임
그렇게 되면 loss 값은 -log(정답 class 확률)이 됨
Softmax loss의 최솟값은 0이고, 최댓값은 무한대임

SVM은 정답 score과 오답 score 간의 margin을 신경쓰고, Softmax는 확률을 구해 -log(정답 class)를 신경씀
Optimization (Gradient Descent, Stochastic Gradient Descent)
최적화는 loss 값을 가장 작게 만드는 위치를 찾는 것임
이를 위해 gradient descent, stochastic gradient descent 등을 사용함
# Gradient Descent
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += -step_size * weights_grad# Stochastic Gradient Descent
while True:
data_batch = sample_training_data(data, 256) # sample 256 examples
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += -step_size * weights_grad # parameter update
데이터셋의 loss를 계산하는 것은 굉장히 오래 걸림
그래서 stochastic gradient descent를 사용하여, 전체 데이터셋의 gradient, loss를 계산하지 않고 minibatch로 나눠서 계산함
Minibatch는 보통 2의 지수로 사용하고, minibatch를 이용하여 loss의 전체 합의 추정치와, gradient의 추정치를 계산함
(+) Image Features
Linear classifier는 raw image pixel을 input으로 받아 처리함
하지만 이는 multi-modality 등 때문에 좋은 방법이 아님
실제로 raw image pixel을 사용하면 classifier가 잘 작동하지 않음


그래서 딥러닝이 흥하기 전엔 (초기 컴퓨터비전 말하는 듯) image의 feature representation을 추출하여 classifier에 집어넣음
Feature representation을 사용하면 선형으로 분리가 가능해져 linear classifer로 잘 분리할 수 있음
Feature representation 예시로는 color histogram, histogram of oriented gradients (HoG), Bag of Words 등이 있음

이미지에서 모든 픽셀에 대해 Hue 값을 뽑아 이미지가 전체적으로 어떤 색인지 확인함

이미지에 전반적으로 어떤 edge가 있는지 확인함

문장을 표현할 때 문장 내 단어의 발생 빈도를 계산하여 feature vector로 사용함

Linear classifier에서는 feature extraction이 이루어진 뒤에 training 동안 update 되지 않음
Neural network에서는 feature을 직접 뽑지 않고, raw image pixel을 집어넣고 weight를 update 함
'Run > Machine Learning' 카테고리의 다른 글
| [Machine Learning] CS231N #6 Training Neural Networks 1 (0) | 2023.10.17 |
|---|---|
| [Machine Learning] CS231N #5 Convolutional Neural Networks (0) | 2023.10.16 |
| [Machine Learning] CS231N #4 Backpropagation and Neural Networks (0) | 2023.10.15 |
| [Machine Learning] CS231N #2 Image Classification (0) | 2023.10.12 |
| [Machine Learning] 3Blue1Brown Neural Networks (1) | 2023.10.11 |